星の運動

《星は楕円運動している》

1. 円の中心は１点である。
2. 星々は中心となる星（地球の場合は太陽）の周囲を上記のように「楕円運動」している。他から働く力はないから、重力と遠心力のバランスのもとに「慣性運動」していると言うことである
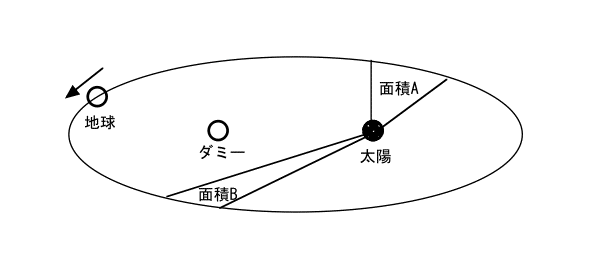
3. 楕円の中心は、上図のように２点あり、その１点を中心として周回している。だから、他の一つの中心はダミーのものとなっている。そのために、もっとも近い点や遠い点が存在する。
4. 何故、この二つの中心の中間点が中心とならないかは、素人には不思議なことである。

《面積速度は一定である》

1. このように、楕円の一つの中心を周回するとすると、重力の影響があるから、その中心に近づくときには重力が強くなり加速度も増し、速度も増す。逆に、離れる場合には加速度はマイナスとなり、速度は減じる。勿論、速度は自分の進行方向に対するものである。
2. ある一定時間をとった場合、面積A=面積Bの関係にある（面積速度一定）。
3. まあ、こんなことは数学に強い人はやってみると良いだろう。
4. とは言え、多くの惑星の運動はかなり円に近いと言って良いだろう。ただし、ハレー彗星のようなものはかなり細長い楕円運動をしている。

《何故楕円運動するか》

1. 太陽のように重力が強い星（重力点）があるとしよう。この重力の場に「何かを・ある速度で・任意の方向に放り出す」としよう。
2. 重力点に完全に横方向に放り出し、かつ放り出し速度が完全に遠心力と重力が釣り合う速度なら放りだしたものは、重力点に対して完全な円運動するのはわかるだろう。
3. しかし、方向は完全な横方向であっても、速度が遅い場合には、遠心力より重力が勝り、円より重力点に近い方向に引きずり込まれ、速度を増すと同時に重力も増し遠心力も増し遠心力が打ち勝ち遠ざかりはじめ、最近点を過ぎると逆に速度が落ち重力も減り、となることはわかる。即ち円にならないことはわかる。
4. 逆に、速度が速い場合も同様である。
5. 外から力は働かない慣性運動であるから、この円でない運動は永久に続いて行く。と言うことで、楕円運動は重力と遠心力くらいがわかっていれば、感覚的に理解できるものと思える。
6. ただし、速度が速すぎると、楕円運動は放物線運動になり一旦近づくことはあっても重力点から離れるばかりになってしまう。「宇宙速度・脱出速度・周回速度」などがあるが、それそれの星や太陽系はその速度を持っている。
7. 蛇足であるのだが、最近宇宙旅行などと言って、高度100キロメートル上空へ2000万円でなどというものがある。これは地球を周回している宇宙ステーションなどとは全く違うものである。飛行機の延長と考えた方がよい。何故ならば、宇宙ステーションなどは地表に対して毎秒10kmなどの速度を持ち、その速度に達するまでのエネルギーを使っているのだが、普通の人の宇宙旅行は100kmまで到達したときの速度は極端に言えば0で良いのである。消費エネルギーは全然違う。だから、飛行機まがいでできるのである。