天体を眺め考える

1. やっと月末に外に持ち出して、月を眺めることにした。感激と言うほどではないが結構よく見える。約150倍ほどの倍率ではっきり見える。翌日インターネットで月の地図入りの写真があるかを調べてみたらあったので、それをプリントしてまた眺めることにした。
   　また問題が生じた。周囲には10階ほどの高い建物が多い。こちらも高いところでなければならない。それで自分の建物の屋上を拠点にしなければならなくなった。


2. まずの目標は「火星・木星・土星の輪」を見ること、それとアンドロメダ銀河を見ることである。また調べなければならない。しかし、どうも都会ではアンドロメダは無理そうである。
   • 私は、とにかく覚えるのは大嫌いである。単に、星座早見で調べ・見た・終わりでは面白くない。星や星雲を眺めようとすると、宇宙・銀河系・太陽系やその惑星などを体系的に頭に入れ、感覚的に望遠鏡を向けられるようにはしたい。
   • そこで、こんなものを作成しながら頭に入れた。目的が頭に概略を入れることであり学者やマニアではない。だから厳密には見ないでいただきたい。
     
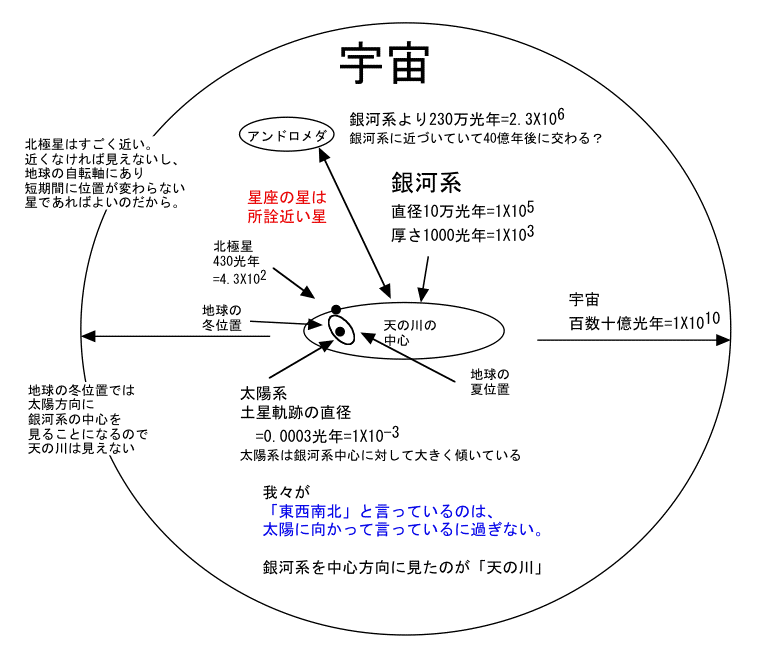
     良いものがあったのでちょっと下記拝借させていただいた。
     
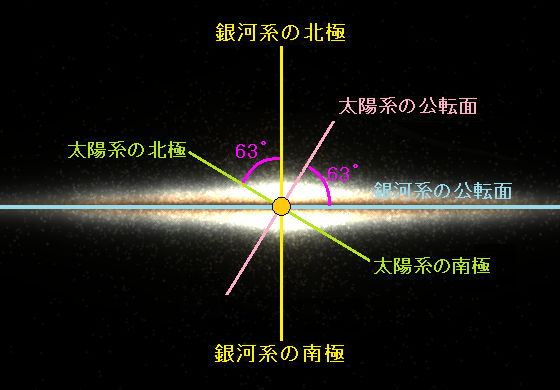
3. さて、この図をベースに「星座早見」の使い方をしっかり頭にいれなければならない。マニアにはどうと言うことはないだろうが「これから」と言う人には参考になるかも知れない。
   • 早見ではベースに丸い円盤があり、そこに我々が見ることができる星々が書かれている。日本人だからほぼ北の部分（この場合は宇宙も太陽系も北はほぼ北）である。
   • ベースの円盤の一番外側には「月と日」がぐるりと書かれている。例えば、６月と１２月は正反対の位置にある。これは、地球が太陽の回りを回っていて、東西は太陽を基準にして言っているので、夏と冬、春と冬では逆の位置に来てしまうからこうなっているのである。
   • ベースの円盤の上には回転する円盤（回転盤とでもしておこう）が固定されている。固定されている部分は、勿論「北極星」である。
   • この外側には「24時間表示」がされている。地球は１日に１回自転しているから、自転（時刻）に合わせて見なければならない。それが、この円盤である。
   • さらに、この回転盤には「楕円形の窓」がある。地球の回転軸というものは、公転面に対して垂直ではなく、23.4度ほど傾いているので見える範囲は異なってくる。そのためにこの窓がある。
   • 障害物がないところで全天を眺めてみればそれは半円球であるはずなのだが、地球の回転軸の傾きから、地球の北半球と言えども１年で見える宇宙は半球以上の部分が見え、それを円盤という平面で表現しているから（北＋αが表示されていて歪んでいる）、見せる範囲の制限が楕円窓で加えられているのである（前の歪みを楕円で補正している）。
   • と言うことであるから、この歪みというものは見る人の目で補正して観察しなければならないものである。
   • 日本語の早見は、日本列島上で利用するものだが、緯度や経度によっても見え方や見える時間が違ってくる。そのために回転盤には、その「経度補正表示」もある。
   　こえが早見の全貌でわかってしまえば単純なものである。でも、この歳71までそんなことを考えたこともなかった。


4. • こんなことを書いていて、ふと思ったことがある。地球は（太陽を固定点とすると）西から東に自転している。太陽に対する公転は北極側から見て、反時計回りである。地球の太陽に対する公転周期は365+1/4日程である。我々はこれで生活している。
   • しかし、もし太陽の回りは回っていても自転はしていない（ある面が常に銀河系の中心を向いている）としよう。これでも夜昼が半年毎に変わる。自転が１年に１回なら、ある面が常に太陽を向いている。と言うことは、太陽に対しては、自転回数は365日と1/4程であっても、銀河系の中心に対しては366日と1/4になっている。
   • こんなことは今まで考えたこともなかったことである（月は地球に対し公転１回自転１回で同じ面を向け続けている、しかし太陽に対しては年十数回の自転がある）。
   星の運動・・・星を眺める前にこんなことは知っておいた方がよいだろう。


5. • 太陽系の惑星を見ようとすると、おおよその位置を直ちに知りたい。
   • 今は、インターネットなどで検索すれば直ちにわかるのだが、土星など一部のものばかりである。
   • おおよそでよいから、土星まででの全惑星がわかるものが欲しい。
   • 惑星全部が、水平の同一面と円軌道としたものでよい。
   • その範囲なら、公転周期と現在位置（初期値）がわかれば計算はエクセルなどで簡単に出来る。
   　と言うことで計算表を作成してみたのが下記の表である。これで大体の位置はわかる。
   この表はインターネットで太陽系のdataを調べ、ある年月日の惑星位置を調べ初期値とし、何日後にどう移動しているかを計算したものである。天文学者ではないし、おおよそがわかえばよいのだから、円軌道でやっている。
   


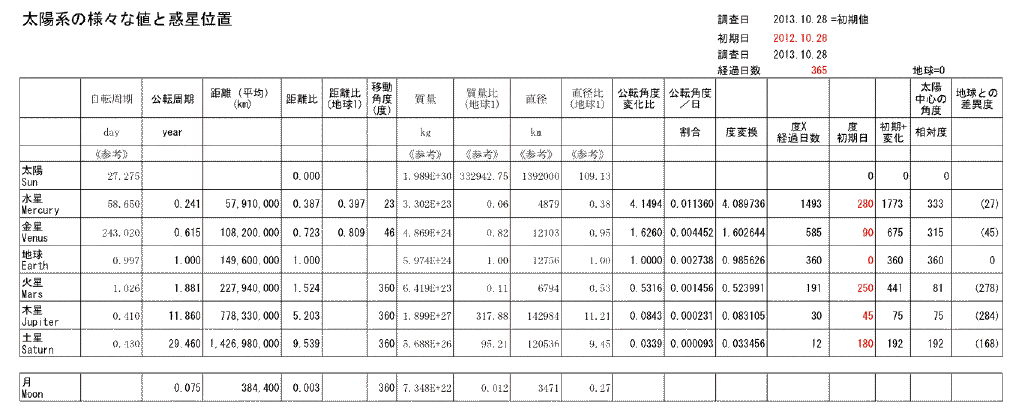
6. 　では、どんな位置に見えるのかを考えると、
   • 地球の自転軸の傾き（23.4度）を考えなければならない。これはこんなことから類推できる。
   • 天の川（銀河系の中心方向）は夏見えるのだが「夏は太陽とは逆方向だから見える」と言うことを頭に置かなければならない。
   • しかも、太陽に向かってどのように傾いているのかを知らなければならない。「日本の夏は太陽が高い」と言うことは、太陽に真正面方向に近いと言うことである。
   　と言うことで、こんな図が書ける。
   


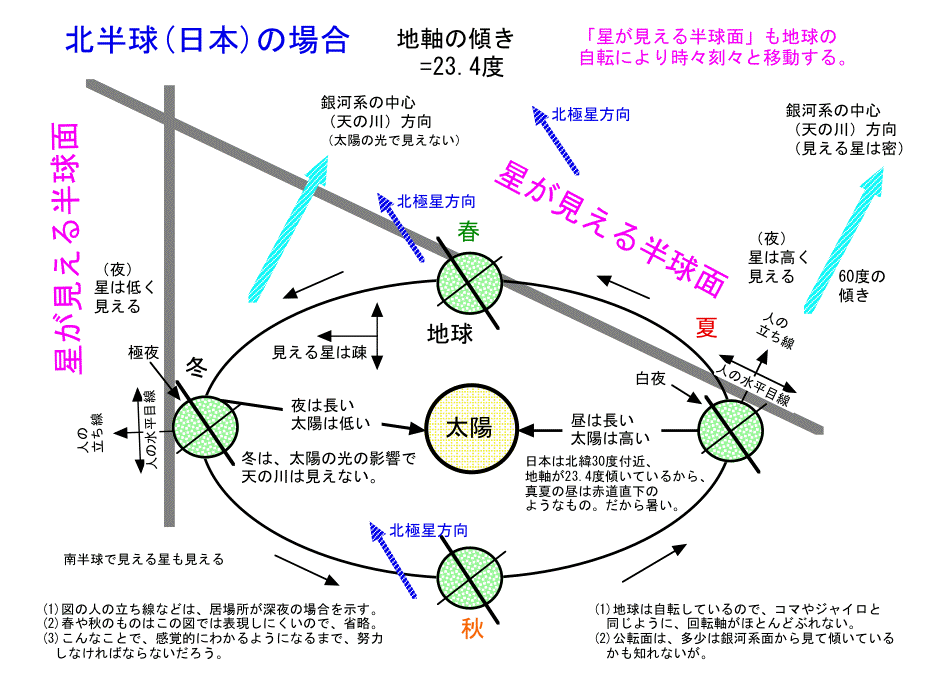
7. 　更に、惑星がどんな移動をするのかを考えてみる。春夏秋冬で星や惑星の高さは違ってくるが、
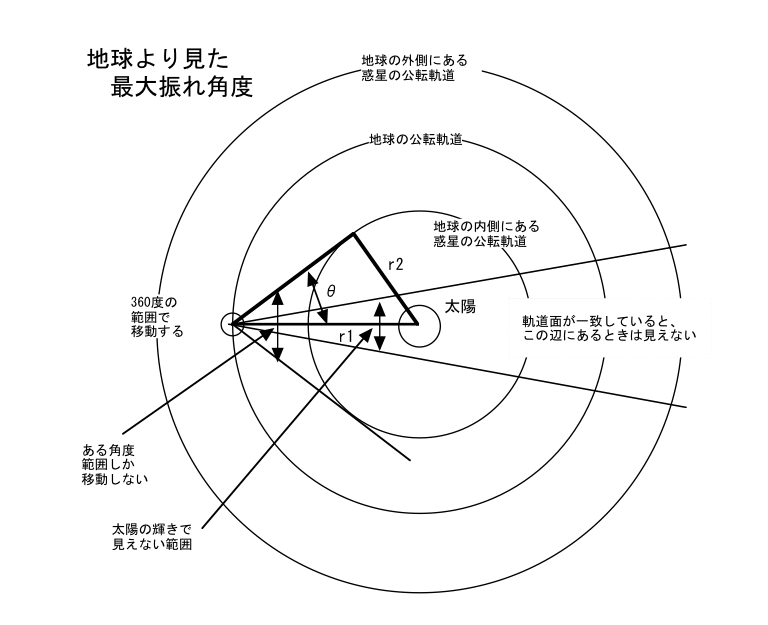
   • 下図のように太陽に近い地球より内側にある惑星は、左右90度の範囲以下で左右に振れて移動しているのかわかる。
   • 同様に、地球より外側にある惑星は360度を移動するのがわかる。
   • かつ、太陽の影響で見えない、見にくい時期がありそうなのもわかる。
   • さて、では水星や金星はどんな範囲で移動しているのかを考える。これには、それぞれと太陽、地球と太陽の距離がわかっていればよい。
   • 水星はsinθ=67910/149600=0.397、金星はsinθ=108200/1496000=0.809
   • 水星はθ=sin^-10.397=23度、金星はθ=sin^-10.809=46度というように太陽を中心として左右に振れることがわかる。
   


8. 上のデータを元にして、単位体積当たりの質量などを調べてみると下記のようになる。最後の列の値だが、地球の質量は5.5程度である。コンクリートの塊などは多分2程度、その程度かと思っていたが、それより大きい。岩石や金属などがあることが理由だろう。
   　ただ、以上のデータは惑星の衛星を考慮したものではないと思うのだが、それはわからない。
   
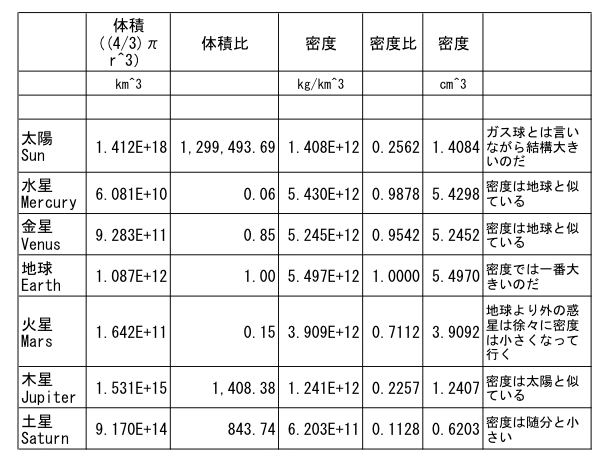
   　世の中には、いろいろな常数がある。光の速度などは簡単だが、普通の人間には「どうやって測定したのかがわからない」ものがほとんどである。太陽や惑星の質量などは、まず距離や公転周期を測定し、公転周期からの遠心力と重力のバランスなどから質量を割り出すのだろう。
   　こんなことは太陽も惑星も点と考えて計算すればよい。しかし、もし地球の中心部に行くことが出来たならば、太陽の重力を考えなければ、四方八方から同じ引力を受け無重力状態になるだろう。こんなことを考えれば中心部の密度はどうなるのかなど不思議なことは沢山ある。


9. 月・・・ついでにこれも調べてみた。


10. こんなことがわかると、惑星の観察には便利なのだろうと思う。逆に、何もわからずインターネット頼みでは、ただ言うなりに星を見ていることになるのだろう。ただ、ここまで書いてきて不思議に思うことがある。上記のような記述がインターネット上で発見できなかったことである（しらみつぶしに調べてはいないが）。常識や当たり前だからなのだろうか。マニアにとってはそうなのだろうが。これからの人のものがもっとあっても良いだろうとも思う。


11. 宇宙とは直接関係はないのだが。虹が出る。虹は７色などと言われている。光の三原色がある。R（赤）G（緑）B（青）の強さと混合で様々な色になる。何故そうなるのかだが勝手にこんな風に考えている。
    
    • いろいろな光は波であり、波長を持つ。
    • それが、混合されると、混合波となる（三角関数の合成）。
    • 混合波の合成波形は、混合したものの和や差などを持つ複雑な波形となる。
    • それが、人間には混合された別の色に見える。
    • 「波長が人間の目で色に変わるのは何故か」については検討もつかない。
    　と言うことである。
    光は際限なく小さな単位になるようである。それでなければはるか彼方から光は届いてこない。無限小だが質量もあるようである。世の中の最小単位のものが光の粒子、でも何かに吸収されてしまえば光はなくなる。と言っても粒子の速度（光の速度）が停止するだけで、存在はある？これがダークマター？、でもそんなものはどんな機械でも測定することも見ることも出来ない？などなど、素人でも疑問がどんどんわき起こる。