古希過ぎ爺の理工趣味

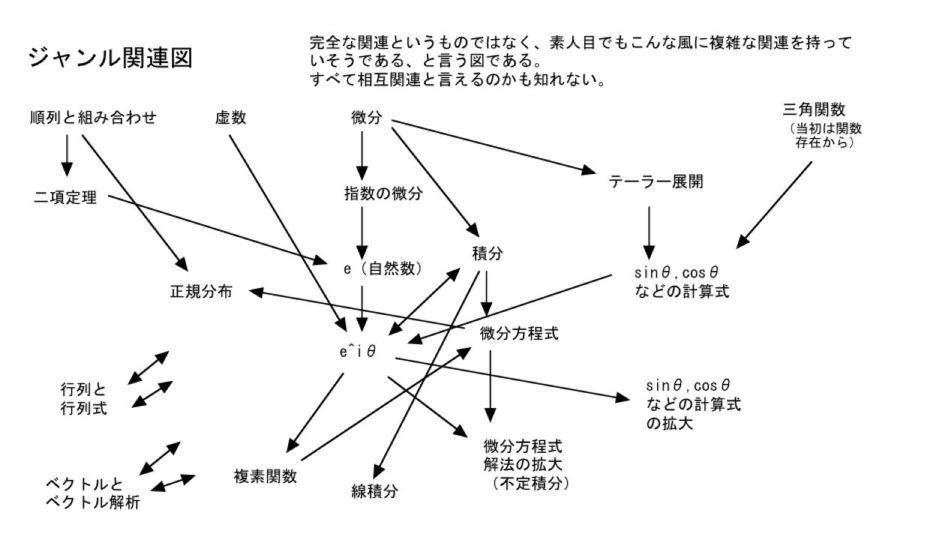
　高校時代にはほとんどないのだが、大学は半部活生活、卒業して以降「あそこでわからなくなった」と言ういくつもの点がある。それを還暦過ぎから気まぐれにおさらいしている。古希も過ぎた。孫でも理工科系に進んだら教えることもあるかな、寿命が持つかな、惚け防止にもなるかなと言う感じなのだが、飽きないからでもある。
　最近は結構わかりやすい本も出ている。インターネットでも様々な説明がある。しかし、本などは紙面の制限もあるだろうから所詮はしょっている。それで、私の頭では「それでも四苦八苦」と言うものが多い。それで、突破するのにあちこちを眺め考え突破する。間違えて理解しているものもあるかも知れない。所詮こんな初心者だが、そんな経過をホームページにしている。
　古希過ぎ爺になると、頭も頭の回転も悪くなり、簡単なことでもつまずいてしまう。だから、自分自身懇切丁寧にやって行かないと理解できない。そんなことは見る人の役に立つかも知れない。間違っていたり、はしょっている点もあるかも知れないが、学生さんなら先生に聞いてもらえばよいだろう。恐ろしいことだが、「機械的に覚え、習慣になったが、根本は理解して居ないことを忘れ、先を過ごす」と言うことがある。学校の先生にもこんな人は居るのではなかろうか。この年齢になると「数ヶ月するとやったことも全く記憶になくなっていた」などもっと恐ろしいことがある。

　当初は、約15年前からhtmlでコツコツ作成してきたのだが、偶然に見る人には便利そうなのでpdfに置き換え中である。
　タイトルだけのものは置き換え未了であるが、コツコツ置き換えたいと思う。ただ、歳も歳でどこまでやれるかもわからない。

ジャンル	タイトル	記事
数学	potential,1/x,e,log,a^x	まず、こんな記述はどうだろう。密接な関係がある。
数学	指数の微分とｅ（ネピア数）	eは、指数の微分を考えれば出てくるものであり、自然界は「指数が基本」を示すものだろう。
数学	1/xの世界の不思議	積分結果はlog(x)、しかし、これはX^(n)の積分の極限から、オーソドックスに導出出来ることがわかった。やって行くと途中に指数の微分が出てきて、ここでeも出てくることになる。しかし、今まで参考でこんな解説を見たこともないのが不思議である。
数学	x^nの微分	nが自然数のときは、簡単に理解できるのだが、有理数や無理数まで拡大した証明は意外に出ていない。微分の初期ではそこまで理解できないので進んでしまい放置されるのだろう。
数学	複素数	「数理上絶対的に正しいもの、それが出てきた場合には何を意味するのか」をしっかりわかっておく必要があるだろう。大学レベルの先生はともかくとして、先生方がどれだけ観念的にわかっているかには大きな疑問がある。
数学	近似の重要性	私は近似というものが昔から好きではない。公式にせよ、何にせよ近似を使わずに理想的に解きたいし、解けるはずと思いたいからである。しかし、あれこれやって行くと、微小区間を扱ったり、いろいろな面で「近似なしでは先に進まない」と言うこともわかってきた。近似式は様々なものがあり、見る気にはならないのだが、認識だけは持っておかなければならない、と言うことがこの年齢になってやっとわかった。
数学	フーリエ級数	比較的簡単なものであり、予定になかったが、後から加えることにした。電気・音・地震など振動現象に共通な関数であるだろう。
数学	オイラーの公式　(e^iθ=cosθ+isinθ)	eがわかり、複素数がわかると次はこれかも知れない。知っている範囲でこんな美しいものはない。三角法定理などは忘れたらこれを思い出すだけでよい。
数学	置換積分＝座標変換？	難しいことではないのだが、簡単な例で教えもせず、いきなりd(sinθ)はcosθdθなどとやられるのは、感覚的な面で理解に苦しむものである。いくかの例で感覚を掴むしかない。
数学	線積分	これを正確に理解しない限り、何事も理解できない。ベクトル解析・複素数などなど
数学	分布・正規分布・ガンマ関数　正規分布（step1）　正規分布（step2）とガンマ関数	二項分布は高校生でもわかる。大学時代は正規分布は「式はこうなる、覚えておけばよい」だったように思う。二項分布を正規化したのがこの式であることもやっと知ったし、これは、確率・二項分布・微積分や微分方程式さらにはガンマ関数などなど広くわからないと理解できないものだったのだ。理解不完全な部分もあるのだが、何とかやってみたというところである。やっと重大な引っかかりがわかった気分になっている。
数学	ベクトル　ベクトルの内積	内積はinner product「内に積もる力」と考えればわかりやすい。
数学	面	Rotationなど理解するためにはx-y-z面を考えなければならなくなる。ところが、私の場合には「面の表現」に惑わされた。私の頭の問題かはわからない。つまらないことだが、こんなところに十分注意しないと先が遅くなる。
数学	Divergence Gradient Rotationの入口　 Divergence & Gradient 　Rotation	あっさり通過しようとすれば、何となく理解したつもりになって先に進むことはできる。しかし、核心まで理解しようとすると少ししつこく探究しなければならない、と言うのがこの項だろう。卒業後使うこともなかったが、この完全な理解なしに先に進むことは出来なかった、電気をやってきたとは言えなかった。それが今頃わかっている。先生も念入りに教えてくれれば良かったのに。先生は頭が良すぎたのだろうか。
数学	ガウスの定理（平面の定理）　グリーンの定理　ストークスの定理	わかってしまえば何ということはないのだが、Greenの定理の理解には時間がかかった。
数学	複素関数	実関数・複素関数がある段階からごちゃ混ぜになって入ってくる。複素関数は習っただけで、学生時代も卒業以降も実務で使ったこともない。微分方程式の一般解が求まる、不定積分が簡単にできる、程度の認識しかないのだが、興味はある。　基礎として「微分の定義→コーシー・リーマンの定理→コーシーの積分定理→正則関数の積分路変形定理→留数定理」などを覚えなければならなそうである。
数学	コーシー・リーマンの定理	この定理を覚えて、やっと複素関数の本格領域に入って行けると言うのだろう。
数学	複素関数	線積分・極・真性特異点・留数など、これだけはおさらいしておきたい。
数学	展開の基礎知識	テーラ展開の理解は容易だが、ローラン展開の理解は難しく、理解を諦めるかも知れない。
数学	留数の応用	定積分、主値積分などは、余裕があったらやってみよう。
数学・遊び	利息や返済金額の計算	昔1980年の40歳頃、借金をするのに「元利均等返済の数式」がわからず、自分で式を考えたものである。
数学・遊び	級数の和を式にする	遊びだがこんな方法がある。
数学	おさらい後記	国は数学系の在り方をどう考えているのだろう。
宇　宙	下記は左記から、見て下さい。ポテンシャルエネルギー、万有引力・引力計算・引力は何故質量が１点集中として、その点間の距離で考えて良いのか？（直行座標と極座標）、加速度が変化するものの移動計算（時間・距離・速度）、
電　気	純電気的なことも別掲にしておこう。この年齢になっておさらいしてみたが、専門でない数学以上に忘れていることがわかった。ただ、家電機器（特に音響系）などには仕事柄学生時代以上に詳しくなっている点もある。

　上記のようなことをやっていると、同じ数学ジャンルでも下記のような範囲をあっちに行ったり、こっちに行ったり、無知を感じ、奥深さを感じる。

　　一応大学出である。学部は理工科・電気である。古希も過ぎて幸い元気な仲間達と飲んだりゴルフしている。仲間達と話していると最近「大学出は頭でっかち」と思えるようになった。最もこれには学部の特性もあるだろうから、電気の世界に限定し、フリーに記述することとしたい。違う学部もあるだろう。

理工系は数学だのが、若い頃得意なのが集まっていた。
卒業時に既に、理工に見切りをつけて、商社など物づくりに疎遠な世界に入った人も居る。最後まで理工人間として残っているのは一握りである。
ゴチョゴチョ物いじりが好きな連中は、一部であって必ずしも物いじりは得意でない人も多い。
特別な天才・秀才ならゴチョゴチョ物をいじりながら片手間で勉強し、難関校にも入るだろうが、一般的な頭ではそんなことをしていたら、難関校には入れない。物いじりは諦めないと入れない。
メーカーなどでは、高専出身者が物づくりの先頭に立ってることが極めて多い。
理系の勉強も出来て就職も良いから来たという人間も多く見ている。
難関校でない人にセンスある人も多い。センスなき難関校出も多く目にしている。

日本はハイテクで稼がなければならない。
戦後は「工」が中心だったかも知れないが、どこでも出来る工の部分には世界各国が台頭している。これからはもっと「先端的ハイテク工」を追求する必要がある。そうなると「理」の追求も益々強化しなければならない。
しかし、頭でっかちでは駄目である。それを支える「技工」ももっと追求しなければならない。ドイツなどにはマイスター精度がある。
大学のある主の学部には「理・工」に「技工」を加えなければならない。試験も分けなければペーパ人間だけが受け入れられてしまう。
更に、理や工の追求には、数学や物理も重要である。しかし、理・工・技工人間のそれらの追求には限界がある。数学者や物理学者を優遇し、それとの連携も重要である。

高校までは「数学は得意」と思っていた。
ところが大学にはいると急にハードルが高くなり、わからないまま試験通過だけを目指し、卒業してしまった。「あそこでわからなくなった」と言うことは、以降も忘れずに残っていた。
しかし、会社に入ってからは業務優先で、時々は思い出すもののおさらいをする時間はなかった。これが自営業になった60歳頃まで続いていた。
還暦過ぎから、少し時間の余裕も出てきた。そこで「今更役立つことはないが、おさらいをしよう、惚け防止くらいにはなるだろう」と言うことになった。
それから十数年、所詮初心者範囲だが、微積分・微分方程式・複素数・ベクトル解析・確率と統計・行列式・などなどあちこちにとびながら、おさらいをしている。やる時期もあるし、まったくやらない時期もある。気分次第である。
おさらいの結果は、ホームページに掲載している。教科書も授業も唐突である場合が多い。「若い人が見て何かの補いになってくれればよい」と思うからである。そんなおさらいの結果を下記に示している。